(本方法将包含在IEC 61400-4第2版中,并于2021年发布。)
风力发电机中,传动系统部件的可靠性是非常重要的。特别是在多兆瓦级的海上风电应用中,意外更换传动系统部件可能产生极高的成本。因此,风电运营商的期望是能预测系统的可靠性。在VDMA的领导下,于2019年10月发表了标准化论文23904“风力发电机的可靠性评估”。
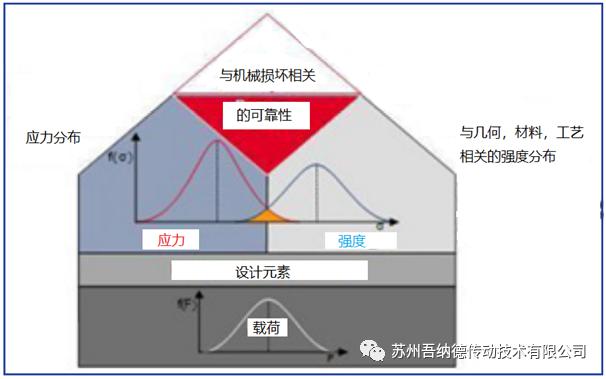
图1 系统的可靠性
到目前为止,风电齿轮箱已按IEC 61400-4标准设计。该规范指定了齿轮箱的所有承载部件的最低安全要求,必须满足各种运行和极端载荷条件。如:齿根和齿面承载能力的最小安全系数的设计依照ISO 6336-3和ISO 6336-2标准,以及胶合和微点蚀的承载能力依据ISO/TS 6336-20或ISO/TS 6336-21和ISO/TS 6336-22标准。轴按DIN 743进行设计,螺栓联接按VDI 2230进行设计,结构件按FKM规范的“钢和铸铁部件的尺寸”和“断裂力学”进行设计,确定计算的边界条件。所有计算方法的共同之处在于它们都是基于安全概念,即:许用载荷是以安全系数的形式来评估出现的载荷的。标准化论文23904提供了一种计算风力发电机齿轮箱可靠性的方法(图1)。该方法本质上是基于Bertsche的统计确定故障概率的原则。
理论计算方法对实际运行中出现的所有失效机理并不是都适用。本方法**于根据公认的技术规范描述的疲劳寿命的失效机理。因此,研究影响可靠性的参数并比较齿轮设计是可能的。目前还不可能绝对预测系统的可靠性。所以,今后必须确定到目前为止还没有计算方法的失效机理或相关统计分布的计算方法。
该方法首先需要确定与系统可靠性相关的功能要素(图2)。通常,这些要素是传递功率零件和支承结构。

图2 功能要素的确定
下一步,基于失效模式分析(FMEA)确定所谓的系统要素;系统要素描述了功能要素的失效机理。例如,齿轮可能由于齿根弯曲疲劳或点蚀损伤而失效(图3)。

图3 系统要素

图4 系统要素的分类
然后对这些系统要素进行分类,所考虑的系统要素被分为与可靠性相关(A1,A2,B)和与可靠性无关(C)(图4)。A1表示有标准计算方法可用的要素(如:ISO 6336),而A2是指没有标准计算方法可用的要素。B类要素的特征是不确定性的失效分布(如:胶合或粘着)。因此,应该用经验和实验来预测这些要素的可靠性。C类要素与系统的可靠性无关,因此不被考虑在计算范围内。在目前的可靠性计算中考虑了A1和部分A2的系统要素。该分类对应于当前的技术状态,如果A2要素可以使用公认的计算方法,则会对其进行调整。
系统的可靠性是由系统各组成部分的可靠性相乘来确定的。这假设了失效模式彼此相互独立,并且失效导致了功能要素的失效(布尔条件)(图5)。


图5 系统可靠性的计算
该方法提供了对A1系统要素的计算方法。
使用3参数威布尔分布计算部件的可靠度R。这些形状参数β、失效概率F(η)= 63.2%的特征寿命η和位置参数γ,在疲劳分析中,通常用于解释无故障时间。可靠性R(t) = 1-F(t)是失效概率的补集。如果在另一个失效概率F(B x )=x%下指定寿命分量B x ,则可以按下式计算寿命B 10 :

本文推荐了形状参数和f tb 。
该方法还为渐开线齿轮的齿根断裂和点蚀失效模式提供了一种扩展的计算方法。基于ISO 6336-6,确定某一载荷谱的损伤总和,并与潜在的韦勒曲线进行了比较。进行迭代,谱随时间变化并计算每个步骤对应的失效概率。由此得到系统要素在整个运行时间内的失效概率(图6)。